Euclidean neural networks
What is e3nn?
e3nn is a python library based on pytorch to create equivariant neural networks for the group \(O(3)\).
Where to start?
Guide to the
e3nn.o3.Irreps: Irreducible representationsGuide to implement a Convolution
The simplest example to start with is Tetris Polynomial Example.
Guide to implement a Transformer
Demonstration
All the functions to manipulate rotations (rotation matrices, Euler angles, quaternions, convertions, …) can be found here Parametrization of Rotations.
The irreducible representations of \(O(3)\) (more info at Irreps) are represented by the class e3nn.o3.Irrep.
The direct sum of multiple irrep is described by an object e3nn.o3.Irreps.
If two tensors \(x\) and \(y\) transforms as \(D_x = 2 \times 1_o\) (two vectors) and \(D_y = 0_e + 1_e\) (a scalar and a pseudovector) respectively, where the indices \(e\) and \(o\) stand for even and odd – the representation of parity,
import torch
from e3nn import o3
irreps_x = o3.Irreps('2x1o')
irreps_y = o3.Irreps('0e + 1e')
x = irreps_x.randn(-1)
y = irreps_y.randn(-1)
irreps_x.dim, irreps_y.dim
(6, 4)
their outer product is a \(6 \times 4\) matrix of two indices \(A_{ij} = x_i y_j\).
A = torch.einsum('i,j', x, y)
A
tensor([[ 0.9392, -1.5069, -0.8065, -0.2333],
[ 1.2374, -1.9854, -1.0626, -0.3074],
[-0.3351, 0.5376, 0.2877, 0.0832],
[ 0.1121, -0.1799, -0.0963, -0.0278],
[-1.6751, 2.6876, 1.4384, 0.4161],
[-0.6226, 0.9990, 0.5347, 0.1547]])
If a rotation is applied to the system, this matrix will transform with the representation \(D_x \otimes D_y\) (the tensor product representation).
Which can be represented by
R = o3.rand_matrix()
D_x = irreps_x.D_from_matrix(R)
D_y = irreps_y.D_from_matrix(R)
plt.imshow(torch.kron(D_x, D_y), cmap='bwr', vmin=-1, vmax=1);

This representation is not irreducible (is reducible). It can be decomposed into irreps by a change of basis. The outerproduct followed by the change of basis is done by the class e3nn.o3.FullTensorProduct.
tp = o3.FullTensorProduct(irreps_x, irreps_y)
print(tp)
tp(x, y)
FullTensorProduct(2x1o x 1x0e+1x1e -> 2x0o+4x1o+2x2o | 8 paths | 0 weights)
tensor([-1.4355, 0.8159, 0.9392, 1.2374, -0.3351, 0.1121, -1.6751, -0.6226,
-0.4208, 0.5451, 0.8336, -0.0839, 0.7261, -1.9685, 0.2152, -1.9742,
-0.2864, -0.0139, 1.1244, 0.6867, 1.8324, 1.1848, 0.6723, 0.2366])
As a sanity check, we can verify that the representation of the tensor prodcut is block diagonal and of the same dimension.
D = tp.irreps_out.D_from_matrix(R)
plt.imshow(D, cmap='bwr', vmin=-1, vmax=1);
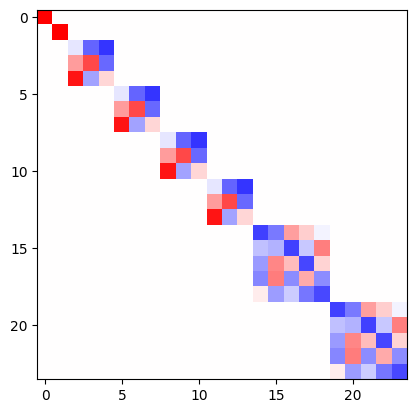
e3nn.o3.FullTensorProduct is a special case of e3nn.o3.TensorProduct, other ones like e3nn.o3.FullyConnectedTensorProduct can contained weights what can be learned, very useful to create neural networks.