Irreducible representations

This page is a beginner introduction to the main object of e3nn library: e3nn.o3.Irreps. All the core component of e3nn can be found in e3nn.o3. o3 stands for the group of 3d orthogonal matrices, which is equivalently the group of rotation and inversion.

from e3nn.o3 import Irreps

An instance of e3nn.o3.Irreps describe how some data behave under rotation. The mathematical describtion of irreps can be found in the API Irreps.

irreps = Irreps("1o")
irreps

1x1o

irreps does not contain any data. Under the hood it is simply a tuple of made of other tuples and ints.

# Tuple[Tuple[int, Tuple[int, int]]]
# ((multiplicity, (l, p)), ...)

print(len(irreps))
mul_ir = irreps[0]  # a tuple

print(mul_ir)
print(len(mul_ir))
mul = mul_ir[0]  # an int
ir = mul_ir[1]  # another tuple

print(mul)

print(ir)
# print(len(ir))  ir is a tuple of 2 ints but __len__ has been disabled since it is always 2
l = ir[0]
p = ir[1]

print(l, p)

1
1x1o
2
1
1o
1 -1

Our irreps means “transforms like a vector”. irreps is able to provide the matrix to transform the data under a rotation

import torch
t = torch.tensor

# show the transformation matrix corresponding to the inversion
irreps.D_from_angles(alpha=t(0.0), beta=t(0.0), gamma=t(0.0), k=t(1))

tensor([[-1., -0., -0.],
        [-0., -1., -0.],
        [-0., -0., -1.]])

# a small rotation around the y axis
irreps.D_from_angles(alpha=t(0.1), beta=t(0.0), gamma=t(0.0), k=t(0))

tensor([[ 0.9950,  0.0000,  0.0998],
        [ 0.0000,  1.0000,  0.0000],
        [-0.0998,  0.0000,  0.9950]])

In this example

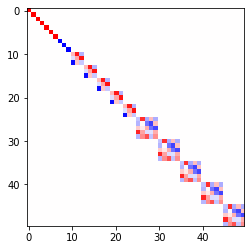
irreps = Irreps("7x0e + 3x0o + 5x1o + 5x2o")

the irreps tell us how 7 scalars, 3 pseudoscalars, 5 vectors and 5 odd representation of l=2 transforms. They all transforms independently, this can be seen by visualizing the matrix

from e3nn import o3
rot = -o3.rand_matrix()

D = irreps.D_from_matrix(rot)

import matplotlib.pyplot as plt
plt.imshow(D, cmap='bwr', vmin=-1, vmax=1);